整数
我们用 -101 来表示二进制下的 -5,但是很遗憾的是,计算机只能理解 1 和 0,并不能理解负号。
一种可行的解决方案是,我们把最高位单独拿出来做符号位,最高位为 0 代表正数,最高位为 1 代表负数,如 00000010 代表 4,而 10000010 代表 -4。这种表达方式称为原码表示法(sign-and-magnitude representation)。一个 n 位的原码能表示 -2^(n-1)+1~2^(n-1)-1 之间的数字,以八位为例,能表示 -127~127。但是这种表示法有一个问题,他无法计算正数和负数的加法,比如 4 + (-4) 用原码计算就成了 00000010 + 10000010 = 10000100 变成了 -8,显然这是不正确的。
为了能够正确计算正数和负数的加法,我们需要使用反码表示法(one's complement representation),我们先把负数的绝对值写出来,再按位取反,即得到它的反码,比如 -4,我们先写出其绝对值 4 的二进制 00000010,再按位取反得到 11111101,这就是它的反码。反码的表示范围同原码。我们再计算 4 + (-4),得到 00000010 + 10000010 = 11111111,最高位是 1,说明是负数,按位取反,得到 00000000,即值为 -0,也就是 0,结果正确。但是反码也存在一个问题,那就是它包含一个正零(00000000)和一个负零(11111111),这在判断相等的时候很容易出问题。
补码表示法(two's complement representation)就是解决所有问题的最终产物,它的步骤类似反码,先写出负数的绝对值的二进制,再按位取反,但是最后补码还要再加一。比如写 -4 的补码,先写4的二进制 00000010,再按位取反得到 11111101,最后再加一得到 11111110,这就是 -4 的补码。在补码表示法中,正数和负数可以正常计算加法,并且只有一个 0。注意,由于补码表示法在表示负数时加一,因此,一个 n 位的补码能表示 -2^(n-1)~2^(n-1)-1 之间的数字,以八位为例,能表示 -128~127,比原码和反码多表示一个负数(-128)。
通常,我们定义正数的原码,反码,补码都是他自身。
在大多数语言中,都会定义 4 字节即 32 位的整数为整型(integer),其表示范围为 -2147483648~2147483647,即 -2^31~2^31-1。对于更高的位数要求,大多数语言都会定义一种 8 字节即 64 位的长整型(long integer),其表示范围为 -9223372036854775808~9223372036854775807。而部分语言如 python 中,它的整数都是高精度整数(high accuracy integer),可以表示任意大小的数值,它通过维护一个链表使用动态内存大小来储存整数。
大端模式与小端模式
假设我们有一个四字节的整数 0x12345678(十六进制),要把它储存在内存中的四个字节,我们一定要以 0x12 0x34 0x56 0x78 的顺序吗?非也!我们也可以反过来,把低位放前面,高位放后面,储存为 0x78 0x56 0x34 0x12。这就是大端模式和小端模式带来的纷争。
大端模式(big-endian),是一种仿照人类的思维方式的二进制储存方式。假设一个四字节的整数 0x12345678(十六进制),依照大端模式储存,它在内存中的储存顺序是:0x12 0x34 0x56 0x78。小端模式(little-endian)则是相反的储存方式,他将低位放在前面,高位放在后面,储存为 0x78 0x56 0x34 0x12。
大端模式的优势在于符号位在第一位,能快速判断正负。小端模式的优势在于,不同字节的整数类型互相转换十分方便,比如 17 不管储存在一字节整数中还是储存在四字节整数中,其数值都在第一字节中,而大端模式下,17 在四字节整数的最后一个字节。
通常来讲,Intel 芯片采用小端模式,ARM 芯片默认采用小端模式,但是可以切换大端模式。而在 C/C++ 语言中,默认小端模式储存,但是在某些单片机上以大端储存,在 Java 语言中,与平台无关总是以大端储存。
小数
接下来我们要处理一个更棘手的问题。。。如何只用 1 和 0 表示出小数及其小数点?
一种方式是定点数(fixed-point number),即,我们固定小数点位于某个特定位置,之后所有程序都按照这个规定来读取小数。比如我们固定一个八位的小数,小数点位于第三位和第四位之间,即前三位为整数部分,后五位为小数部分,那么一个二进制值 11001001 就被视为 110.01001 来读取,得到 6.28125。不过这种方式显然是有很大的问题的。首先他能表示的数值范围太小了,其次它固定了小数位的精度,而通常我们对小数位数的精度要求是动态的。
现在我们讨论一下对小数精度的要求。我们知道,一个非常大的数加上一个非常小的数造成的影响可以忽略不计,因此,通常对精度的要求是对于所有有效数字位数的。例如对于一个 10^20m 量级的星系距离,我们可能要求它精度有整数位就够了,因为零点几米对于星系距离而言实在是太小了,甚至我们可能只要求它前 15 位精确就行了,后面的5位整数的精确度都不在乎。而对于一个 10^-5m 量级的机械零件而言,我们对其的精度要求可能到小数点后 10 位,毕竟哪怕是 1 微米对于它而言都是相当大的。
这时候,我们就要请出科学计数法(scientific notation)了,科学计数法是形如 a.bbbb x 10^c 形式的数值,小数点前有且只有一位非 0 值。例如 156724.122 写成科学计数法是 1.56724122 x 10^5,而 0.0002447 写成科学计数法是 2.447 x 10^-4。使用科学技术法的好处在于,这种表达形式很好地体现出了数值的精度,而不用去考虑究竟是小数点后的第几位。
而我们现在常用的二进制小数表示法,浮点数(floating-point number)就是二进制下的科学计数法。浮点数的通式是 1.aaaa x 2^b,由于小数点前有且只有一位非 0 值,对于二进制而言只能是 1,所以也可以省略这个 1,写作 .aaaa x 2^b,不过在计算数值时要记得这里还有个 1。仍然以 6.28125 举例,它的二进制 110.01001 写作科学表达式是 1.1001001 x 2^2,或者省略小数点前的 1 写作 .1001001 x 2^2。而储存这个科学计数法到纯二进制中,我们只需要储存三个值即可:
- 符号(sign),代表整个数值的正负。
- 指数(exponent),即
1.aaaa x 2^b中的b。 - 尾数(fraction),即
1.aaaa x 2^b中的aaaa。这样的话,我们就要把一个数值分开不同的位来分别储存这些值。
现在绝大多数编程语言都是用 IEEE 二进制浮点数算术标准(IEEE 754)所定义的浮点数表示方式。IEEE 754 规定了两种形式的浮点数:单精度浮点数(single-precision float-point number)通常简称单浮点(float)和双精度浮点数(double-precision float-point number)通常简称双浮点(double)。
对于单精度浮点数,使用 4 字节即 32 位储存,能表示的数值范围大约是 -3.4 x 10^38 ~ 3.4 x 10^38:
- 第一位即最高位是符号位,0 代表正数,1 代表负数。
- 第 2~9 位一共 8 位表示指数,指数使用偏移法,即把 [-126, 127] 全部偏移 127 到 [1, 254],再转换为二进制储存,例如
-56应该偏移到71储存为1000111。注意 0 和 255 有特殊用法,不在可选范围内,用于表示零,正无穷,负无穷,NaN 等等特殊值,有兴趣可以去了解一下。 - 剩下的 23 位为尾数部分,不储存小数点前的 1,大约对应十进制的 6~7 位精度。
对于双精度浮点数,使用 8 字节即 64 位储存,能表示的数值范围大约是 -1.7 x 10^308 ~ 1.7 x 10^308:
- 第一位即最高位是符号位,0 代表正数,1 代表负数。
- 第 2~12 位一共 11 位表示指数,同样把 [-1022, 1023] 全部偏移 1023 到 [1, 2046] 再储存,0 与 2047 用作特殊值的储存。
- 余下的 52 位为尾数部分,不储存小数点前的 1,大约对应十进制的 15~16 位精度。
字符
关于二进制如何储存字符,我在以前的章节中已经多次介绍,这里做个总结和扩展。
- ASCII:全称美国信息交换标准代码(American Standard Code for Information Interchange),使用一个字节即八位表示一个字符,但是只使用
0~127之间的数字,不使用128~255之间的数字。现代字符编码大都会选择兼容 ASCII,将自己的前 127 位保持与 ASCII 一致。 - IBM扩展字:在 ASCII 的基础上,定义了
128~255之间的字符。 - ANSI:不同国家或地区所制订的不同的编码标准,如 ANSI 在简体中文系统中指 GBK,在日语系统中指 shift-JIS,在繁体中文系统中指 big5。通常,ANSI 会让
0x00~0x7F保持和 ASCII 一致,并且样只使用一字节来储存,而0x80~0xFFFF则使用两个字节储存。例如汉字“中”在 GBK 中以0xD6D0两字节储存。ANSI 是 Windows 系统所使用的编码方式。 - Unicode:即统一码。Unicode 是一种旨在统一所有语言的所有字符的文字编码,以满足跨语言、跨平台进行文本转换、处理的要求。通常,我们使用
U+为前缀表示 Unicode 码,比如汉字“中”的 Unicode 码是U+4E2D。 UTF-8:即 8-bit Unicode Transformation Format,是一种针对 Unicode 的可变长度字符编码,它通过增加一些特殊位,使自己可以使用不同字节来表示 Unicode 编码。这样做的好处是,表示 ASCII 的部分仍然只需要一个字节,降低英文文本的文件大小,另外他可以向后扩展到 6 字节一个字符,以适应越来越多的 Unicode 编码(现在 Unicode 字符的数量两字节已经放不下了)。
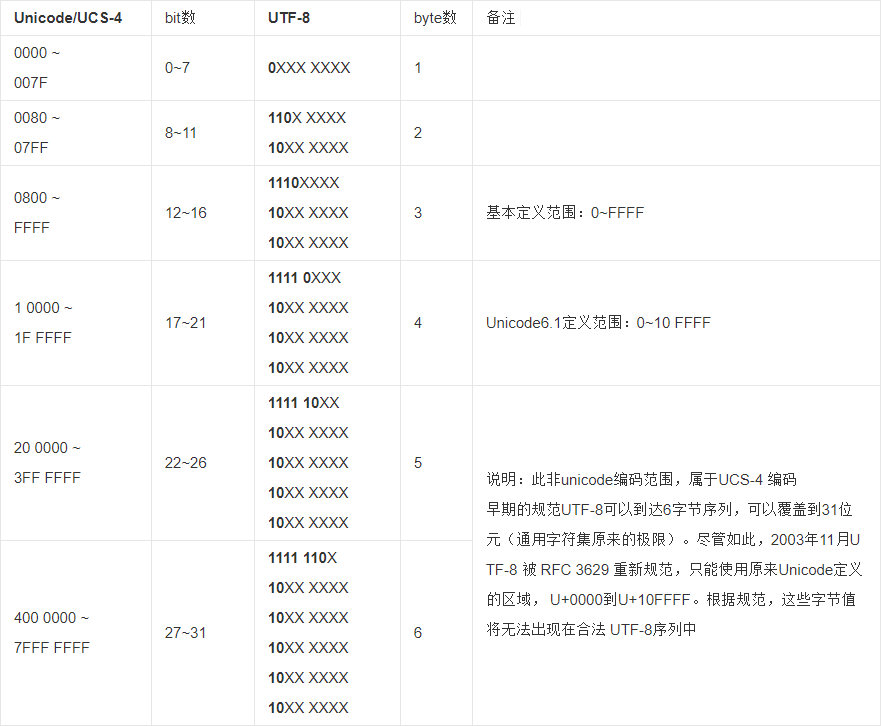
根据上图,我们可以找到“中”的 UTF-8 二进制表示形式。“中”的 Unicode 码
U+4E2D位于0800~FFFF区,因此占用三个字节,把“中”的 Unicode 码写成二进制,即:0100 1110 0010 1101,注意 UTF-8 三字节表示格式即1110 XXXX 10XX XXXX 10XX XXXX中,我们可以发现 X 的数量刚好是 16 个,把“中”的 Unicode 码的二进制一位一位地填入到 UTF-8 中,得到1110 0100 1011 1000 1010 1101,整理为十六进制就是0xE4B8AD。UTF-8 是几乎所有的 Linux 系统所使用的编码方式。- UTF-16:即 16-bit Unicode Transformation Format,是一种定长度字符编码,固定使用两字节表示一个字符,即使是 ASCII 部分也使用两个字节。除此之外,还有 UTF-32,以定长度的四字节表示一个字符。
- BOM:即字节顺序标记(Byte Order Mark),是 Unicode 下用来表示字符以大端模式还是以小端模式储存的一种特殊隐藏字符,出现在字符流或者文本文件的最开头处。BOM 的值为
0xFEFF,在 UTF-16 中,如果读到0xFE 0xFF代表大端模式,如果读到0xFF 0xFE则代表小端模式,在 UTF-32 中,读到0x00 0x00 0xFE 0xFF表示大端模式,读到0xFF 0xFE 0x00 0x00表示小端模式。而在 UTF-8 中,我们使用特殊规定的顺序来表示 Unicode,因此并不需要指定字节顺序标记,但是我们可以使用 BOM 来告诉 Windows 系统,我们这个字符流或者文本文件是用 UTF-8 编码的,而不是 ANSI 编码。在 UTF-8 中的 BOM 值为0xEFBBBF,通常我们称以 BOM 开头的 UTF-8 编码为 UTF-8 with BOM。
按位存储
在某些类型的游戏中,我们可能会让角色拥有多种状态,例如攻击 BUFF,防御 BUFF,恢复 BUFF,中毒,烧伤,冻伤,迟缓,等等,如果我们要传递给 script 去处理各种状态的话,我们不得不给每个状态都使用一个脚本参数,随着游戏进一步开发,状态还可能越来越多,维护起来也愈加麻烦。
这种时候,我们就可以借用按位存储的思想。我们知道,布尔值只需要占用一个比特,而GML的实数类型提供一个 64 比特的整型,我们可不可以把这个整型拆开来用,每一个比特都用来代表一个状态,这样让所有的状态同时储存在同一个变量中呢?当然可以。
首先,我们初始化一个状态变量,然后指定每一个状态所在的比特位。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 这是状态变量,储存所有的状态
status = 0;
// 这是攻击BUFF,占用最后一位
ATK = 1;
// 这是防御BUFF,占用倒数第二位
DEF = 1 << 1;
// 这是恢复BUFF,占用倒数第三位
RECOV = 1 << 2;
// 这是中毒状态,占用倒数第四位
POISON = 1 << 3;
// 这是烧伤状态,占用倒数第五位
BURN = 1 << 4;
// 这是冻伤状态,占用倒数第六位
FROZE = 1 << 5;
// 这是迟缓状态,占用倒数第七位
SLOW = 1 << 6;
增加一种状态我们可以使用:
1
status |= ATK;
同时增加多个状态,我们可以这样写:
1
status |= (POISON | SLOW);
去掉一种状态我们可以使用:
1
status &= ~FROZE
同时去掉多种状态我们可以使用:
1
status &= ~(ATK | DEF);
判断是否处于某种状态我们使用:
1
if (status & RECOV)
判断是否同时处于多种状态我们使用:
1
if (status == status | (BURN | FROZE))
判断是否处于任意一种状态我们使用:
1
if (status & (BURN | FROZE))
判断处于且只处于某种状态我们使用:
1
if (status == ATK)
判断同时处于且只处于多种状态我们使用:
1
if (status == (ATK | DEF))